Mini: 3D Rotation

How to rotate with Euler Angles and Axis Angles

What’s kickin’ chicken?

Previously, I wrote about 2D rotations and how rotations can be stacked for 3D Euler Angles (yaw, pitch, and roll):

In 3D, there are several other ways to rotate. First, we’ll start with Euler Angles.

Euler Angles

One simple way to solve 3D rotation is with a series of 2D rotations on each axis XYZ.

As previously covered, 2D rotation looks like this:

mat2 rotate2D(float angle)
{
    return mat2(cos(angle), -sin(angle), sin(angle), cos(angle));
}

When you want to rotate a vector around an axis line, say the z-axis, for example, it’s as simple as doing a 2D rotation on the x and y axes, leaving the z-axis unchanged. Then you can rotate again on another axis to add another degree of rotation.

Source: en.Wikipedia.org.

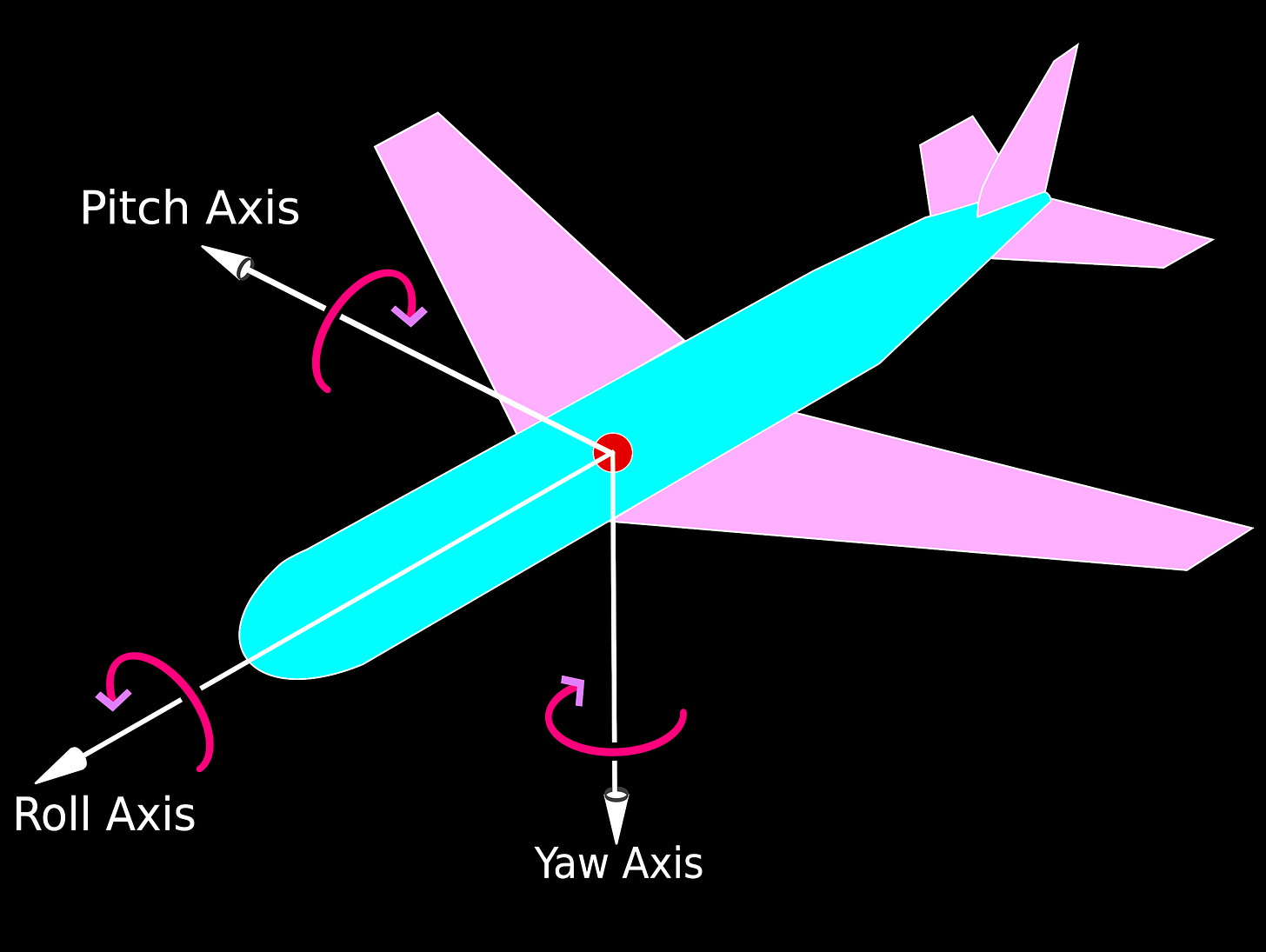
You could rotate the plane by applying roll, then pitch, then yaw. For example, depending on the axes, it might look something like this:

//Roll (for x-axis)
vector.yz = rotate2D(ROLL) * vector.yz;

//Pitch (for y-axis)
vector.xz = rotate2D(PITCH) * vector.xz;

//Yaw (for z-axis)
vector.xy = rotate2D(YAW) * vector.xy;

Note: The order of the rotation is very important, and the following rotation can be reversed by reversing the order and swapping mat * vec with vec * mat.

This type of rotation is easy to understand and implement, but it has a few drawbacks in some contexts:

• Uses more operations and steps than necessary. It can be simplified further.

• Rotating about an arbitrary axis is not always obvious.

• Doesn’t blend orientations well.

• 90-degree turns can cause gimbal lock.

If you don’t care about those concerns, then you may stop here. For the rest of us, let’s go a step further.

Axis Angle

When you need to rotate around an arbitrary axis, you need this formula (learned from Fabrice Neyret’s code golfing):

//Rotate vector "vec" with angle "ang" around the "axis"
vec = mix(dot(vec, axis) * axis, vec, cos(ang)) + sin(ang) * cross(vec, axis);

That is a little overwhelming at first, so let’s break this down into byte-sized pieces. For this formula to work correctly, we need the axis vector to be a unit vector (with a length of 1.0 units), and “vec” can be whatever coordinates we want to rotate. “ang” is the rotation angle in radians.

Let’s focus on this part:

dot(vec, axis) * axis,

The Dot Product here is finding how far our vector is along the axis and translating that many units in the axis direction. For example, let’s say we have

vec = vec3(1, 2, 3) and axis = vec3(0, 0, 1)

This formula finds how far vec3(1, 2, 3) is in the z axis, which is 3 units, then we move 3 units in the z axis to get vec3(0, 0, 3). You can think of this as the center point that we are rotating around. We want the x and y to change, but not the z. This is just like our Euler Angle example, except that it generalizes to any axis direction!

Now, with that context, let’s look at the whole mix formula:

mix(dot(vec, axis) * axis, vec, cos(ang))

Here we are mixing between the axis center point and the vector. It oscillates between the original vector and the inverted vector across from the axis center point.
This is like the x-axis of our 2D rotation, but for an arbitrary axis.
Finally, we add the sine with a cross product:

 + sin(ang) * cross(vec, axis)

I haven’t covered the cross product in detail yet, but for our purpose now, we can think of it as finding the perpendicular vector. For

cross(vec3(1,0,0), vec3(0,1,0)) we get vec3(0,0,1)

It’s the perpendicular vector of the two vectors (multiplied by their magnitudes and the sine of the angle between them).

So for cross(vec, axis), we get the perpendicular vector to the axis. We multiply this by sine, just like we would with the y-axis of a 2D rotation. Same idea, but for the arbitrary axis!

Source: Eucliedeanspace.com

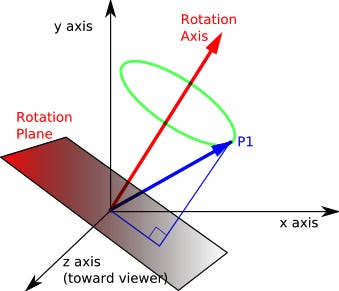
It’s difficult to illustrate, but you can imagine the rotation axis as defining the place that the vector rotates on. When you rotate around, you rotate from the original point to its perpendicular and opposite points along that plane.

This solves most of the drawbacks, is more efficient, blends better, and avoids gimbal lock, but sometimes you need to interpolate between two orientations (especially in video games). The next step will be quaternions, which deserve a separate tutorial on their own. I’ve tried to find good examples that clearly explain how they work, but I was unsuccessful, so I’ll have to write one myself.

Conclusion

At the end of the day, rotation happens at one plane at a time. In 2D, it’s easy, as there are only two axes to work with. In 3D (and higher dimensions), it becomes a little more complex as there any many different ways to rotate.

Euler Angles are simple to understand and work with because they’re just a series of XYZ axis rotations. It works well in video game contexts because you might only need yaw or pitch and yaw rotation. When you want to rotate in an arbitrary direction, you can use Axis Angles. They are relatively simple, clean, and easy. Beyond this, we have quaternions, which have their uses in animations (blending together better), but I’ll leave that for another day.

Extras

Max Slater’s Exponentially Better Rotations - an overview of different rotation techniques, how they interpolate, and going beyond quaternions

That’s all for tonight. Have a great weekend!