Mini: Imagination
Tips and tricks for more vividly imagining your shaders
Hi folks!
Today’s tutorial is a bit different. We’re taking an abstract look at the shader creation process: How to turn an idea in your head to code, as well as how to interpret code more easily. Over the years I’ve developed several ways of thinking that help me to solve new problems in my head and save time.
There are a few math tricks that can be used as building blocks to make almost anything you can think of! Let’s jump in!
Fields
So first thing we need to look at, is vector fields. They’re fundamental to shader programming. If you’re like me, reading the Wikipedia page on vector fields, will make your brain a bit fuzzy.
If you have a solid math background, this may be helpful to you, but honestly most of us forgot what all these terms mean. Don’t worry. You don’t need a background in Calculus to understand this, but you might accidently learn some Calculus as a byproduct. You might know some of the following section, but I’ll go over it again briefly to make sure we’re on the same page.
Coming from GML (or any non-shading language) you’re trained to think of code as executing one command at a time, sequentially. You probably have heard that the GPU that it computes millions of commands simultaneously (in parallel). When I first heard of this, I just assumed it was like the CPU, but much faster. Here’s the part I didn’t fully grasp: GPUs are designed to execute the same, relatively simple commands millions of times using varying inputs (like pixel coordinates or frame time).
So while CPU is great at handling a bunch of if-statements or complicated math, the GPU thrives when the process for every vertex/pixel is identical, just starting with different inputs. For example, you might output a color gradient like so:
//Divide the fragment coordinates by the window resolution
//so that they range from 0 to 1
vec2 uv = gl_FragCoord.xy / u_resolution;
//Set the red and green channel to uv x and y values.
gl_FragColor = vec4(uv.xy, 0.0, 1.0);Coming from a GML coding perspective, I’d think of gl_FragCoord as two variables with an x and y value. But here’s the interesting part: gl_FragCoord is not a single value, but rather a range of vector values. So for fragment/pixel 0,0, uv is computed as vec2(0.0,0.0) / u_resolution, pixel 1,0 is vec2(1.0,0.0) / u_resolution and so on for all the pixels visible on screen! This one line could compute 256 different values at 16x16 resolution, or may 2,073,600 values at 1920x1080 resolution!
In other words, one formula can describe an unlimited number of pixels, simply by changing the input parameters like gl_FragCoord or uniforms like u_resolution.
People often say that branching (if-statements) are bad for GPUs. You don’t need to worry about branching too much as long as you take care with the parallel nature of the GPU. For example, you don’t want to have a unique if-statement for every individual pixel because at that point you’re not doing parallel computing and your CPU would be a better candidate. You want to get good at reducing the unique edge cases in your shaders by using formulas that work on all pixels.
Suppose you want to display a white square. Here’s a naive approach:
//Fragment coordinates centered at (200, 200)
vec2 p = gl_FragCoord.xy - 200.0;
//Set the default color to white
gl_FragColor = vec4(1.0);
//Check 100 pixels in all directions
if (p.x > +100.0) gl_FragColor = vec4(0.0); // Right side
if (p.x < -100.0) gl_FragColor = vec4(0.0); // Left side
if (p.y > +100.0) gl_FragColor = vec4(0.0); // Top side
if (p.y < -100.0) gl_FragColor = vec4(0.0); // Bottom sideThis is totally acceptable for such simple code, but you can imagine if each case required more computation, it would be more costly than it needs to be.
With a little more thought, we can do all of these directional checks in just one step:
//Fragment coordinates centered at (200, 200)
vec2 p = gl_FragCoord.xy - 200.0;
//Set the default color to black
gl_FragColor = vec4(0.0);
//When clamped "p" is the equal to unclamped "p", then we're inside the range
if (clamp(p, vec2(-100.0), vec2(+100.0)) == p)
{
gl_FragColor = vec4(1.0);
}Gradients
It might be helpful to think of vector fields as gradients. gl_FragCoord’s x component starts at 0.5 and increases 1 unit per pixel towards the right side of the window.
”v_vTexcoord” measures the texture coordinates in texel units starting from the top-left to bottom-right. Using length(x) gets you a radial gradient centered at (0,0) in whatever units you may choose.
It’s often helpful to visualize your variables. If I don’t know how large or small the values might be, I’ll often try multiplying/dividing it by some magic numbers until I find something that is useful. Example:
gl_FragColor = vec4(p.x / 1000.0, 0.0, 0.0, 1.0);In fact, this leads me straight into my next point!
Domains And Ranges
Every mathematical function/expression has a domain and range. The “domain” is basically the range of acceptable inputs. For example, sqrt(x) only works when x >= 0.0. asin(x) only works with x >= -1.0 and x<=1.0 or a domain of [-1, 1]. It’s always a good idea to be aware of the values you feed into your functions. You should never feed negative “x” values into pow(x, y), because it will not work correctly in most implementations!
“Range” tell us the range of outputs that a function or expression can have. abs(x) will always return a value greater than or equal to 0.0, so never negative. sin(x) will return a number between -1.0 and +1.0 (including -1.0 and +1.0). It’s often helpful to think of the range of your input values like gl_FragCoord which starts at vec2(0.5, 0.5) and ends at the WINDOW_RESOLUTION - vec2(0.5, 0.5). We can use this range to track the range of all subsequent ranges. Like here:
vec2 p = gl_FragCoord.xy - 200.0;So if we wanted to map to the vec2(0.0) to vec2(1.0) range we could do this:
//Remapping "p" from [0.5, res-0.5] to [0.0, 1.0]
vec2 uv = (p + 200.0 - 0.5) / (u_resolution - 1.0);
//Or a common close approximation:
vec2 uv = (p + 200.0) / u_resolution;
//Now if we display these values, we can see the entire range:
gl_FragColor = vec4(uv.xy, 0.0, 1.0);Anytime you need to remap some value “x” from any range [a, b] to any other range [c, d], you can use this simple formula!
remap(a, b, c, d, x) = (x - a) / (b - a) * (d - c) + c;How does this work? Well the “(x - a) / (b - a)” part converts x from [a, b] range to the [0, 1] range. You can think of it as (x - range_start) / range_width which is how it ensures x starts at 0 and ends at 1. The “* (d - c) + c” is simple the same thing but done in reverse with the new range! I use these all the time and it’s super helpful to use along side mix()!
Periods
Functions like cos, sin, mod, fract and etc., are all periodic, meaning they repeat themselves. fract(0.5) = 0.5, but so does fract(1.5), fract(2.5) and so on forever. fract(x) has period of 1 because the output repeats ever 1 unit input.
Here’s an illustration:
sin(x), cos(x), tan(x) all have a period of Tau or Pi*2 (6.2831…).
fract(x) has a period of 1.
mod(x, y) has a period of “y”.
Anytime you need repetition in your shader, you’ll probably need one of these functions! This repeated output can then be used as an input into another function.
Inigo Quilez wrote a great article on this topic which is worth checking out.
Foundational Functions
GLSL doesn’t have a lot of functions. Here’s a full list of the ones supported in GameMaker. There are several of these functions that I never use, but some of them are absolutely fundamental to nearly every shader. Let’s go over some of those.
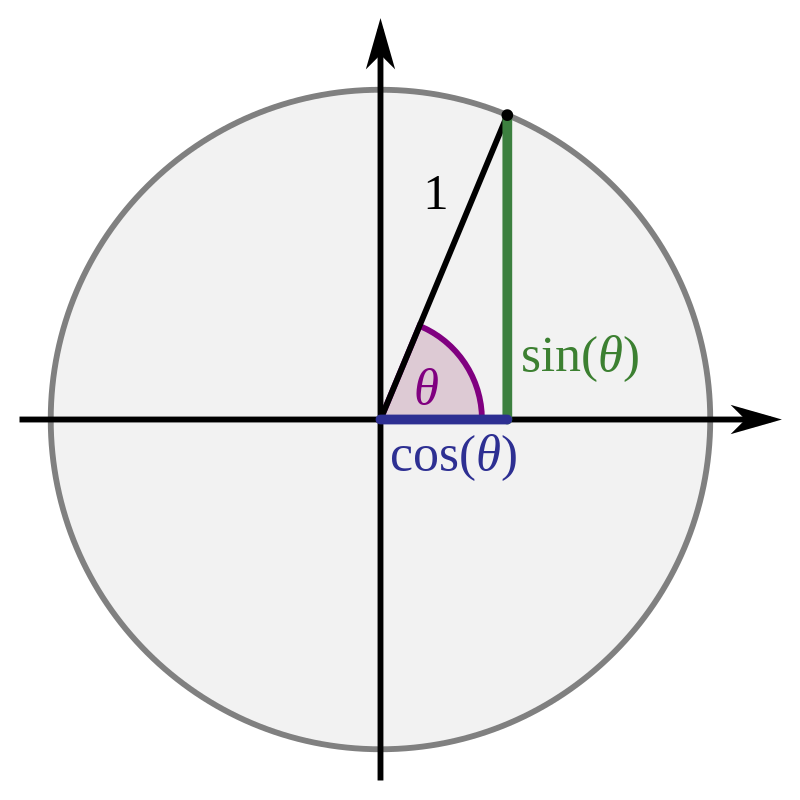
Sin, Cos
You might think of sine and cosine as oscillating waves:
As you can imagine, this is useful for simulating waves in wind or water. This is the foundation of many noise functions because the non-linear nature helps cover up many patterns:
//Classic high-frequency noise function
return fract(sin(p.x*12.9898 + p.y*78.233) * 43758.5453);Or you might think of cosine as the x-axis sine as the y-axis (inverted in GM):
So incase you don’t use trigonometry functions much basically “vec2(cos(angle), - sin(angle))” is the coordinate for a point revolving around 0,0. Sin and cos assume a radius of 1, but you can multiply these by your desired radius.
Don’t forget, sin and cos use radians, so they range from 0 to Tau (6.2831) instead of 0 to 360! You can convert degrees to radians using “radians(deg)”!
I did an entire tutorial on rotation here:
To summarize, if you need smooth waves, white noise, revolving points or rotation, look no further than sin and cos!
Dot
Dot products are another fundamental tool for your mathematical arsenal.
I’ve done a full tutorial just on the math of dot products here!
To recap, dot(a, b) is computed as the sum of the components of a * b:
float dot(vec a, vec b)
{
return a[0] * b[0] + a[1] * b[1] + ...a[n] * b[n];
}You can find the distance a vector stretches along the the x-axis by getting vector.x, but what about an arbitrarily defined axis?
Well, you can with dot like so: dot(vector, normalize(axis))
Think of this like a ruler measuring the vector from whatever axis you choose.
If you need to know how aligned to normalized vectors are, you can do so with dot(a, b)! This will return 1.0 if they are perfectly aligned, 0.0 if perpendicular and -1.0 if opposite. This actually the cosine of the angle between the two vectors!
This is most commonly used for direct lighting:
float light = max(-dot(normal, light_dir), 0.0);It can also be used for computing luma, or light attenuation, but I think you get the picture!
Acos, Asin, Atan
If the dot product is the ruler, the inverse trigonometry functions are the protractors (they measure the angle). acos(x) takes a value between -1 and +1 and returns the angle, in radians, of cos(angle) which equals x. So acos(0.0) returns pi/2.0 or 90 degrees because cos(pi/2.0) == 0.0. This pairs very nicely with the dot product of two normalized vectors.
Note: Because cosine is periodic and symmetrical cos(pi*1.5), cos(pi*2.5)… all equal 0.0. For this reason the function has a range of [0, pi]. asin(x) is similar but offset pi/2 or 90 degrees, so it has a range of [-pi/2, +pi/2].
While I don’t use tan(x) very often I do use atan(y, x) quite often! asin and acos have limited ranges, but atan can return the angle for a vector in any quadrant, by supplying both the x and y components. Take note of the argument order and that +y is up in trigonometry.
Pow
We’ve talked about linear remapping, but what about non-linear? Well here’s where pow(base, exp) is your friend!
Here’s a simple radial gradient:
It starts and ends at the same place for the red, green and blue channels, but the the blue diminishes quickly, the green is neutral and red is slow to diminish.
This is achieved by giving each channel a unique power exponent. The red channel is the sqrt, making it brighter towards the edges, green is unchanged and the blue channel is squared Making it only visible in the center.
You can use exponentiation to emphasize darkness or brightness depending on your needs.
I could go on, but I need to wrap this tutorial up. If there’s interest, I may do a follow up.
Conclusion
So to quickly summarize everything we went over today:
Think in vector fields, not in binaries. GPUs flow from pixel to pixel and directing that flow the way you want, is everything! Gradients are everywhere!
It’s helpful to think about the acceptable domains (input ranges) of your functions and expressions as it can tell you what values to expect and prevent errors. You don’t want to feed negative numbers in
sqrt(x).Be aware of the output ranges of your functions/expressions. If you let them get out of control, you’ll get unexpected results. Don’t forget to remap ranges wherever needed!
You can always create repetition using periodic functions like mod. Very helpful when you need something to tile.
Sine and cosine are great for waves, revolutions and rotations.
The dot product is your ruler whenever you need to measure things.
Inverse trig functions are your protractors!
Use exponentiation to give brightness more or less weight.
And that covers it! I hope this gave you some new perspective and will help you on your shader journey.
Extra
If you’re still hungry to learn more, I highly recommend this talk by Alexander Sannikov about a wide range of graphics techniques used in Path of Exile.
In future tutorials, I’d like to include some extra articles/videos/papers that I find throughout the week like this one. If you find something you’d like to share, send me a message!
Have a great weekend!
-Xor









The video URL is dead but I believe this is the same one:
https://www.youtube.com/watch?v=TrHHTQqmAaM