Mini: OkLab
A more natural way to blend colors
Hello there,
Today, I want to talk about color blending, and it’s many oddities.
On the top, you have a standard RGB color blend between yellow and blue using mix.
Notice how it goes from yellow to middle gray and then to blue.
On the bottom, you have steady increments of the lightness and chroma, which produces a more natural looking transition.
Today, we’re going to look at three different ways to describe color and how it can be useful to convert between them.
Color Spaces
Remember Vector Spaces? Well, color vectors can be transformed to different color spaces too. For example, you can convert Red, Green and Blue to Hue, Saturation and Value (RGB to HSV) or HSV back to RGB. There are plenty of examples of color conversions like that, so I won’t cover those here, but I do want to talk about a relatively new one that doesn’t have as examples or resources. First, you need to understand sRGB.
sRGB
Stands for “Standard Red, Green and Blue”. This is generally the default color space used for anywhere from hexadecimal colors like #FF8811 to gl_FragColor’s output. sRGB was originally designed for CRT displays, which had a non-linear relationship between voltage and brightness. This saved processing because the colors did not have to be decoded, but it means sRGB does not model light physics or human perception (although it’s sort of close).
sRGB has an exponential relationship to brightness, which means if we do all of our calculations in sRGB, we’re skewing the results towards black. See the CRT gamma below:
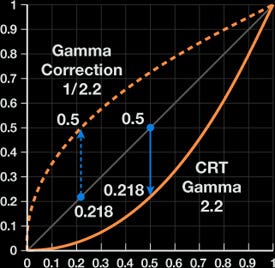
This is where gamma correction comes into play.
Linear RGB
If we want to do things like lighting or color blending properly, we have to invert the sRGB gamma, to make brightness linear again, then do lighting/blending, before converting back to sRGB.
Unfortunately, nothing in color theory is concrete, but the most common gamma value is 2.2. Games often make this value adjustable because it varies from place to place. We can convert to and from sRGB by using pow():
//Convert sRGB to linear RGB
vec3 linear_from_srgb(vec3 rgb)
{
return pow(rgb, vec3(2.2));
}
//Convert linear RGB to sRGB
vec3 srgb_from_linear(vec3 lin)
{
return pow(lin, vec3(1.0/2.2));
}Blending
Now, if we convert our sRGB colors to linear RGB, do the blending in linear RGB and then convert back, we generally get better results. But is RGB really the best way of blending colors? As we saw above, if we mix yellow and blue half-and-half, we get gray. We know that red and green are perceived as lighter colors than blue, so speaking in perceptual terms, we should expect the midpoint to be brighter.
Also, what’s up with colorfulness and chroma? Both ends have color, but the midpoint loses all color because in RGB, the RG and B cancel out in the middle, as though they are perceived exactly the same.
Human color perception is more complicated than that…
I won’t repeat all the details here, but if you’d like to learn more, I recommend reading Björn Ottosson’s full article on the topic. It does a good job of explaining the issues with sRGB and Linear RGB. Now enter
OkLab
OkLab is a color space created to approximate human perception of lightness and chroma. If we convert our linear RGB colors to OkLab, mix them and then convert them back to sRGB, we get perceptually even gradient (approximately):
Björn Ottosson has found some “magic” numbers from the data that models this pretty well with just a couple of matrices and a pow():
//By Björn Ottosson
//https://bottosson.github.io/posts/oklab
//Shader functions adapted by "mattz"
//https://www.shadertoy.com/view/WtccD7
vec3 oklab_from_linear(vec3 linear)
{
const mat3 im1 = mat3(0.4121656120, 0.2118591070, 0.0883097947,
0.5362752080, 0.6807189584, 0.2818474174,
0.0514575653, 0.1074065790, 0.6302613616);
const mat3 im2 = mat3(+0.2104542553, +1.9779984951, +0.0259040371,
+0.7936177850, -2.4285922050, +0.7827717662,
-0.0040720468, +0.4505937099, -0.8086757660);
vec3 lms = im1 * linear;
return im2 * (sign(lms) * pow(abs(lms), vec3(1.0/3.0)));
}
vec3 linear_from_oklab(vec3 oklab)
{
const mat3 m1 = mat3(+1.000000000, +1.000000000, +1.000000000,
+0.396337777, -0.105561346, -0.089484178,
+0.215803757, -0.063854173, -1.291485548);
const mat3 m2 = mat3(+4.076724529, -1.268143773, -0.004111989,
-3.307216883, +2.609332323, -0.703476310,
+0.230759054, -0.341134429, +1.706862569);
vec3 lms = m1 * oklab;
return m2 * (lms * lms * lms);
}It’s important to note that OkLab is designed to work with linear RGB, so make sure to convert to linear RGB and back to sRGB when you’re done. In OkLab, the X component represents lightness (0 to 1), the Y component represents green/magenta chroma (-0.5 to 0.5) and the Z component represents blue/yellow chroma (-0.5 to 0.5).
If you have a few minutes, give Björn’s article on OkLab a read. It’s very interesting to see the process behind how this was designed.
One more thing! Since OkLab will often be used for blending colors, I want to share this optimized OkLab mix function written by Inigo Quilez:
//By Inigo Quilez, under MIT license
//https://www.shadertoy.com/view/ttcyRS
vec3 oklab_mix(vec3 lin1, vec3 lin2, float a)
{
// https://bottosson.github.io/posts/oklab
const mat3 kCONEtoLMS = mat3(
0.4121656120, 0.2118591070, 0.0883097947,
0.5362752080, 0.6807189584, 0.2818474174,
0.0514575653, 0.1074065790, 0.6302613616);
const mat3 kLMStoCONE = mat3(
4.0767245293, -1.2681437731, -0.0041119885,
-3.3072168827, 2.6093323231, -0.7034763098,
0.2307590544, -0.3411344290, 1.7068625689);
// rgb to cone (arg of pow can't be negative)
vec3 lms1 = pow( kCONEtoLMS*lin1, vec3(1.0/3.0) );
vec3 lms2 = pow( kCONEtoLMS*lin2, vec3(1.0/3.0) );
// lerp
vec3 lms = mix( lms1, lms2, a );
// gain in the middle (no oklab anymore, but looks better?)
lms *= 1.0+0.2*a*(1.0-a);
// cone to rgb
return kLMStoCONE*(lms*lms*lms);
}This takes linear colors converts them to OkLab for the mixing and then returns the linear color result, which saves on some extra math and complexity.
Here’s a ShaderToy demo I put together!
Conclusion
OkLab is one of the best ways of balancing colors in perceptually consistent ways.
Like compare this gradient’s lightness and saturation consistency to standard HSV:
While OkLab is not a perfect approximation, it does a pretty good job and can easily be reversed, which is important for color space transformations. I’ll be looking into using this for a color quantizing tool I’m working on. It may be useful to pick the most perceptually distinct colors when reducing the palette, and this will be how I can.
You may be able to use this to pick color palettes for your games or to help with accessibility for color blindness. There are many possibilities here, and I hope this gives you some ideas.
Extras
Björn Ottosson has also OkLab replacements for HSV and HSL that also are designed for matching human eye perception.
Nvidia released a detailed article on Gamma Correction.
That’s it for this week! I’m taking the rest of December off to focus on family and some personal projects. I have an exciting guest writer who will be filling in for me next time. Big thank you to everyone who reads these, and especially the supporters who help keep this going. Until next time, Merry Christmas and Happy New Year!
—Xor





