GM Shaders Mini: Vector Spaces
Examining "texture space", "screen space", "world space", and more.
Hi friends. Maybe you’ve heard terms like “view space”, “model space” or “screen space”, but you’re not sure what it all means exactly? This is what we’ll be exploring today. For our purposes, “spaces” can be thought of as coordinate systems, which can be rotated, translated, scaled and skewed. We’ll go over the most important vector spaces, what they’re used for, and how to utilize them in both 2D and 3D contexts.
Coordinates
When I was new to shaders, I based everything off of “v_vTexcoord” (texture coordinates). This was adequate for most of my needs, but then I’d occasionally run into some strange scaling and aspect ratio issues which had trouble conceptualizing.
I wrote specifically about those problems here if that interests you:
GM Shaders Mini: Scaling
Today I want to go a bit deeper, building on the context we’ve established so far. The best place is to start with a familiar space, called “texture space”.
Texture Space
When you’re working with v_vTexcoord, you’re working in texture space. The x and y axes are oriented with the texture. +X is always right and -X is always left on the texture, no matter how the sprite is rotated in the room. Texture space is measured in texel units, so if you stretch your sprite, it has no effect on the range of texel values, but it will stretch that range across more pixels.
Screen Space
gl_FragCoord are the x and y fragment (pixel) coordinates relative to the screen, where (0, 0) is the top-left corner. If you stretch your sprite, it will actually expand the range of values, because it is covering more pixels.
It doesn’t matter if you translate, scale or rotate your view, (0,0) will always be the top-left corner of the screen.
Note: GM is vertically flipped compared to ShaderToy and some other applications. -Y is up in GM.
Object Space
Also called “model space”, object space are the coordinates relative to the object’s origin. If you rotate your object, the coordinates rotate also, so the up-axis is relative to the object’s orientation (and can be flipped).
GM doesn’t have a direct way to access object space with 2D draw functions like draw_sprite() or draw_rectangle(). That’s because the transformations are baked into the vertex positions before it even gets to the vertex shader. So if you need to work in object space, you can pass transformations as uniforms or convert the texture space to pixels in object space. In 3D, with vertex buffers, you get the model space coordinates for free from the in_Position attribute, before it gets transformed by matrices.
World Space
World space can be thought of as the position in the room. (0,0) is always the top-left corner of the room (or (0,0,0) in 3D). As mentioned draw_* pre-bakes the world-space transformation in in_Position so you don’t need to do any calculations in 2D.
If you do use matrix_set(matrix_world, matrix) in GML, then you can multiply the in_Position by the built-in matrix GM_MATRICES[MATRIX_WORLD]:
vec4 world = GM_MATRICES[MATRIX_WORLD] * vec4(in_Position, 1.0);Notice this is a 4D matrix times a 4D vector. The 4D part allows for translations (shifting the position), which cannot be done with a 3D matrix. If you ever don’t want to shift, you can set the w-component to 0.0, which multiplies the translation by 0.0.
It’s important to note that matrix * vector will probably give different results to vector * matrix. At some point, I’d like to do a full tutorial on matrices, but for now, just know that it changes the order of the multiplication.
View Space
View space (sometimes called “eye space” or “camera space”) builds upon world space. A view matrix maps a world space position to a position relative to the view camera. In this case (0,0) is the center of the screen, +Y is up (opposite of screenspace) and in 3D +Z is forward. In 2D (or with orthographic projections), this will be in pixel units, just reoriented and translated. This extremely useful for effect’s like fog, where you can use the view space z component to get the depth.
Generally you want to use GM_MATRICES[MATRIX_WORLD_VIEW] which already multiplies the world and view matrices together, but you can also use GM_MATRICES[MATRIX_VIEW].
vec4 view = GM_MATRICES[MATRIX_WORLD_VIEW] * vec4(in_Position, 1.0);This is also the bedrock for complicated effects like deferred rendering and and many “screenspace” effects.
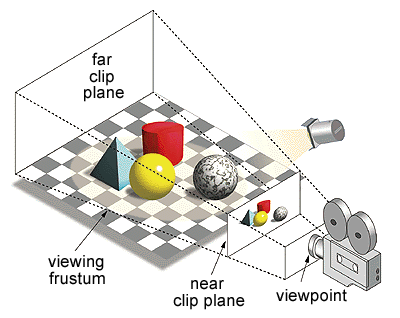
Projection Space
The projection matrix is perhaps the hardest to understand, but is arguably the most important. gl_Position expects coordinate values ranging from -1 to +1 (also known as clip space). All fragments outside this range are clipped to save computation.
The projection matrix accounts for aspect ratio, z-near and z-far clipping planes and with orthographic projections, size. With a perspective matrix, it handles the Field Of View. 4D matrix multiplication cannot directly create a square frustum because it requires division (to create the perspective effect).
Thankfully, we have one trick we can use. Remember that "w” component, which was always 1.0? Well, we can actually use that as the perspective factor for dividing all the other x, y and z components. This is why gl_Position expects a vec4, for the clip space xyz and perspective factor (which does the dividing internally).
Here’s an example using the projection matrix:
vec4 proj = GM_MATRICES[MATRIX_WORLD_VIEW_PROJECTION] * vec4(in_Position, 1.0);Conclusion
To summarize, spaces are a helpful way to think about vectors and their ranges. They can manipulate the orientation, scales, positioning and skewing (like with perspective frustums). It’s a great idea to familiarize yourself with these different spaces, which are so crucial to many of advanced effects like fog, SSAO, shadow mapping and more.
I hope this can serve as a strong foundation for the 2D game developers who want a deeper understanding of the underlying process. Maybe some of you can use this as a starting point for 3D!
Extras
As usually, I’d like to include some extra resources that I found helpful this week.
LearnOpenGL has a great tutorial in-depth on these matrices, so if you’re stuck on anything or what to go further, I recommend checking it out!
Here’s a great video on pixel art upscaling by t3ssel8r
Acerola made a great video explaining color spaces here
This is the part where paid subscribers can help me pick the next tutorial!
That’s it for today! Thanks for reading! Have yourself a great weekend
-Xor